海量字符串检索之二 布隆过滤器

发表于 更新于 分类于 Disqus： 本文字数： 10k 阅读时长 ≈ 17 分钟

海量字符串检索是很考验算法效率的工作。Trie树和PAT树常用，但是内存占用严重。在垃圾邮件过滤或网络爬虫这种不要求检索结果完全正确的场景下，布隆过滤器是个很好的选择。

Hash函数

Hash（中译为哈希，或者散列）函数在计算机领域，尤其是数据快速查找领域，加密领域用的极广。其作用是将一个大的数据集映射到一个小的数据集上面（这些小的数据集叫做哈希值，或者散列值）。Hash table（散列表，也叫哈希表），是根据哈希值(Key value)而直接进行访问的数据结构。也就是说，它通过把哈希值映射到表中一个位置来访问记录，以加快查找的速度。时间复杂度只有O(1).

哈希函数有以下两个特点：

  • 如果两个散列值是不相同的（根据同一函数），那么这两个散列值的原始输入也是不相同的。
  • 散列函数的输入和输出不是唯一对应关系的，如果两个散列值相同，两个输入值很可能是相同的。但也可能不同，这种情况称为“散列碰撞”（或者“散列冲突”）。
    解决冲突的方法有许多，如向左或向右移位，拉链法等等。在数据量不大的情况下，Hash函数作为查找的解决方法看上去是很美好的。然而，数据量大了之后呢。不妨设想下面的应用场景。

假设要你写一个网络蜘蛛（web crawler）。由于网络间的链接错综复杂，蜘蛛在网络间爬行很可能会形成“环”。为了避免形成“环”，就需要知道蜘蛛已经访问过那些URL。给一个URL，怎样知道蜘蛛是否已经访问过呢？稍微想想，就会有如下几种方案：

  1. 将访问过的URL保存到数据库。
  2. 用HashSet将访问过的URL保存起来。那只需接近O(1)的代价就可以查到一个URL是否被访问过了。
  3. URL经过MD5或SHA-1等单向哈希后再保存到HashSet或数据库。
  4. Bit-Map方法。建立一个BitSet，将每个URL经过一个哈希函数映射到某一位。

以上方法在数据量较小的情况下都能完美解决问题，但是当数据量变得非常庞大时问题就来了。

方法1的缺点：数据量变得非常庞大后关系型数据库查询的效率会变得很低。而且每来一个URL就启动一次数据库查询是不是太小题大做了？

方法2的缺点：太消耗内存。随着URL的增多，占用的内存会越来越多。就算只有1亿个URL，每个URL只算50个字符，就需要5GB内存。

方法3：由于字符串经过MD5处理后的信息摘要长度只有128Bit，SHA-1处理后也只有160Bit，因此方法3比方法2节省了好几倍的内存。

方法4消耗内存是相对较少的，但缺点是单一哈希函数发生冲突的概率太高。还记得数据结构课上学过的Hash表冲突的各种解决方法么？若要降低冲突发生的概率到1%，就要将BitSet的长度设置为URL个数的100倍

实质上上面的算法都忽略了一个重要的隐含条件：允许小概率的出错，不一定要100%准确！也就是说少量url实际上没有没网络蜘蛛访问，而将它们错判为已访问的代价是很小的——大不了少抓几个网页呗。

上面所举的爬虫只是一个例子，在允许少量错误的情况下，布隆过滤器将是最好的选择。

布隆过滤器（Bloom Filter）

布隆过滤器（Bloom Filter）是由布隆（Burton Howard Bloom）在1970年提出的。它实际上是由一个很长的二进制向量和一系列随机映射函数组成，布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法，缺点是有一定的误识别率（假正例False positives，即Bloom Filter报告某一元素存在于某集合中，但是实际上该元素并不在集合中）和删除困难，但是没有识别错误的情形（即假反例False negatives，如果某个元素确实没有在该集合中，那么Bloom Filter 是不会报告该元素存在于集合中的，所以不会漏报）。

基本思想

如果想判断一个元素是不是在一个集合里，一般想到的是将所有元素保存起来，然后通过比较确定。链表，树等等数据结构都是这种思路. 但是随着集合中元素的增加，我们需要的存储空间越来越大，检索速度也越来越慢。不过世界上还有一种叫作散列表（又叫哈希表，Hash table）的数据结构。它可以通过一个Hash函数将一个元素映射成一个位阵列（Bit Array）中的一个点。这样一来，我们只要看看这个点是不是 1 就知道可以集合中有没有它了。这就是布隆过滤器的基本思想。

优缺点

  • 优点——相比于其它的数据结构，布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插入/查询时间都是常数。另外, Hash 函数相互之间没有关系，方便由硬件并行实现。布隆过滤器不需要存储元素本身，在某些对保密要求非常严格的场合有优势。
  • 缺点——误算率（False Positive）是其中之一。随着存入的元素数量增加，误算率随之增加。但是如果元素数量太少，则使用散列表足矣。另外，一般情况下不能从布隆过滤器中删除元素. 我们很容易想到把位列阵变成整数数组，每插入一个元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全的删除元素并非如此简单。

误算率（False Positive）分析

一个Bloom Filter有以下参数：

m | bit数组的宽度（bit数）
n | 加入其中的key的数量
k | 使用的hash函数的个数
f | False Positive的比率

假设 Hash 函数以等概率条件选择并设置 Bit Array 中的某一位，m 是该位数组的大小，k 是 Hash 函数的个数，那么位数组中某一特定的位在进行元素插入时的 Hash 操作中没有被置位的概率是：1 - 1/m

那么在所有 k 次 Hash 操作后该位都没有被置 “1” 的概率是：(1 - 1 / m)^k

如果我们插入了 n 个元素，那么某一位仍然为 “0” 的概率是：(1 - 1 / m) ^ k*n

因而该位为 “1”的概率是：1 - (1 - 1 / m) ^ k*n

现在检测某一元素是否在该集合中。标明某个元素是否在集合中所需的 k 个位置都按照如上的方法设置为 “1”，但是该方法可能会使算法错误的认为某一原本不在集合中的元素却被检测为在该集合中（False Positives），该概率由以下公式确定：

1 - (1 - 1 / m) ^ k*n ≈ (1 - e ^ (-k * n / m)) ^ k

其实上述结果是在假定由每个 Hash 计算出需要设置的位（bit） 的位置是相互独立为前提计算出来的，不难看出，随着 m （位数组大小）的增加，假正例（False Positives）的概率会下降，同时随着插入元素个数 n 的增加，False Positives的概率又会上升，对于给定的m，n，如何选择Hash函数个数 k 由以下公式确定：

m / n * ln2 ≈ 0.7 * m / n

此时False Positives的概率为：2 ^ -k ≈ 0.6185 ^ (m / n)

而对于给定的False Positives概率 p，如何选择最优的位数组大小 m 呢，

m = -n * lnp / (ln2) ^ 2

上式表明，位数组的大小最好与插入元素的个数成线性关系，对于给定的 m，n，k，假正例概率最大为：(1 - e ^ (-k * (n + 0.5)/(m - 1))) ^ k

值得注意的是，k值并非越大越好。可以证明，当 k = ln(2) * m/n 时出错的概率是最小的。

操作

1.加入字符串

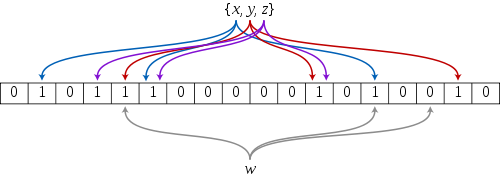
为了表达S={x1, x2,…,xn}这样一个n个元素的集合，Bloom Filter使用k个相互独立的哈希函数（Hash Function），它们分别将集合中的每个元素映射到{1,…,m}的范围中。

当我们往Bloom Filter中增加任意一个元素x时候，我们使用k个哈希函数得到k个哈希值，然后将数组中对应的比特位设置为1。即第i个哈希函数映射的位置hashi(x)就会被置为1（1≤i≤k）。

注意：如果一个位置多次被置为1，那么只有第一次会起作用，后面几次将没有任何效果。在下图中，k=3，且有两个哈希函数选中同一个位置（从左边数第五位，即第二个”1”处）。

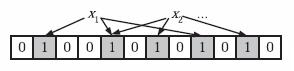
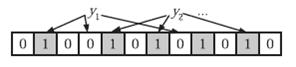
2. 检查字符串是否在集合中

在判断y是否属于这个集合时，我们只需要对y使用k个哈希函数得到k个哈希值，如果所有hashi(y)的位置都是1（1≤i≤k），即k个位置都被设置为1了，那么我们就认为y是集合中的元素，否则就认为y不是集合中的元素。下图中y1就不是集合中的元素（因为y1有一处指向了“0”位）。y2或者属于这个集合，或者刚好是一个false positive。

3. 删除字符串

通常，字符串加入了就被不能删除了，因为删除会影响到其他字符串，且无法判断删除字符串是否真在集合内。实在需要删除字符串的可以使用Counting bloomfilter(CBF)，这是一种基本Bloom Filter的变体，CBF将基本Bloom Filter每一个Bit改为一个计数器，这样就可以实现删除字符串的功能了。

实现

C语言内，并没有定义Bitmap这个容器，所以需要自己实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX 268435456

/*init bitmap*/
unsigned char * bitmap_init(int size){
	int bytes;
	unsigned char * p = NULL;
	if(size % 8 == 0) 
		bytes = size / 8;
	else 
		bytes = size / 8 + 1;
	p = (unsigned char *)malloc(bytes);
	if(NULL == p)
		return NULL;
	memset(p, 0, bytes);
	return p;
}

/*set flag on a certain index bit*/
int bitmap_set(unsigned char * bitmap, int index, int flag){
//index range should have been checked outside!
	int seg = index / 8;
	int off = index % 8;
	unsigned char p =  0x1<< off;
	if(flag == 1)
		bitmap[seg] |= p;
	else if(flag == 0)
		bitmap[seg] &= ~p;
	else
		return 0;
	return 1;
}

/*get flag on a certain index bit*/
int bitmap_get(unsigned char * bitmap, int index){
///check index range outside first!
	int seg = index / 8;
	int off = index % 8;
	unsigned char p = 0x1 << off; 	int tmp = bitmap[seg] & p; 	return tmp > 0 ? 1 :0;
}
/*free bitmap*/
void bitmap_free(unsigned char * bitmap){
	free(bitmap);
	*bitmap = NULL;
}

之后，通过位图的置位和取位即可完成Bloom Filter的插入和检测操作。Hash函数选取如下（实际上，可以通过一个函数生成k个独立的哈希函数，存在优化空间）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
unsigned int RSHash(char* str, unsigned int len)
{
   unsigned int b    = 378551;
   unsigned int a    = 63689;
   unsigned int hash = 0;
   unsigned int i    = 0;

   for (i = 0; i < len; str++, i++)
   {
      hash = hash * a + (*str);
      a = a * b;
   }

   return hash;
}
/* End Of RS Hash Function */

unsigned int JSHash(char* str, unsigned int len)
{
   unsigned int hash = 1315423911;
   unsigned int i    = 0;

   fo r(i = 0; i < len; str++, i++)
   {
      hash ^= ((hash << 5) + (*str) + (hash >> 2));
   }

   return hash;
}
/* End Of JS Hash Function */

unsigned int PJWHash(char* str, unsigned int len)
{
   const unsigned int BitsInUnsignedInt = (unsigned int)(sizeof(unsigned int) * 8);
   const unsigned int ThreeQuarters     = (unsigned int)((BitsInUnsignedInt  * 3) / 4);
   const unsigned int OneEighth         = (unsigned int)(BitsInUnsignedInt / 8);
   const unsigned int HighBits          = (unsigned int)(0xFFFFFFFF) << (BitsInUnsignedInt - OneEighth);
   unsigned int hash = 0;
   unsigned int test = 0;
   unsigned int i    = 0;

   for(i = 0; i < len; str++, i++) {
      hash = (hash << OneEighth) + (*str);
      if((test = hash & HighBits) != 0) {
         hash = (( hash ^ (test >> ThreeQuarters)) & (~HighBits));
      }
   }

   return hash;
}
/* End Of  P. J. Weinberger Hash Function */

unsigned int ELFHash(char* str, unsigned int len)
{
   unsigned int hash = 0;
   unsigned int x    = 0;
   unsigned int i    = 0;

   for (i = 0; i < len; str++, i++) {
      hash = (hash << 4) + (*str);
      if ((x = hash & 0xF0000000L) != 0) {
         hash ^= (x >> 24);
      }
      hash &= ~x;
   }

   return hash;
}
/* End Of ELF Hash Function */

unsigned int BKDRHash(char* str, unsigned int len)
{
   unsigned int seed = 131; /* 31 131 1313 13131 131313 etc.. */
   unsigned int hash = 0;
   unsigned int i    = 0;

   for(i = 0; i < len; str++, i++) {
      hash = (hash * seed) + (*str);
   }

   return hash;
}
/* End Of BKDR Hash Function */

unsigned int SDBMHash(char* str, unsigned int len)
{
   unsigned int hash = 0;
   unsigned int i    = 0;

   for(i = 0; i < len; str++, i++) {
      hash = (*str) + (hash << 6) + (hash << 16) - hash;
   }

   return hash;
}
/* End Of SDBM Hash Function */

unsigned int DJBHash(char* str, unsigned int len)
{
   unsigned int hash = 5381;
   unsigned int i    = 0;

   for(i = 0; i < len; str++, i++)
   {
      hash = ((hash << 5) + hash) + (*str);
   }

   return hash;
}
/* End Of DJB Hash Function */

unsigned int DEKHash(char* str, unsigned int len)
{
   unsigned int hash = len;
   unsigned int i    = 0;

   for(i = 0; i < len; str++, i++)
   {
      hash = ((hash << 5) ^ (hash >> 27)) ^ (*str);
   }
   return hash;
}
/* End Of DEK Hash Function */

unsigned int BPHash(char* str, unsigned int len)
{
   unsigned int hash = 0;
   unsigned int i    = 0;
   for(i = 0; i < len; str++, i++)
   {
      hash = hash << 7 ^ (*str);
   }

   return hash;
}
/* End Of BP Hash Function */

unsigned int FNVHash(char* str, unsigned int len)
{
   const unsigned int fnv_prime = 0x811C9DC5;
   unsigned int hash      = 0;
   unsigned int i         = 0;

   for(i = 0; i < len; str++, i++)
   {
      hash *= fnv_prime;
      hash ^= (*str);
   }

   return hash;
}
/* End Of FNV Hash Function */

unsigned int APHash(char* str, unsigned int len)
{
   unsigned int hash = 0xAAAAAAAA;
   unsigned int i    = 0;

   for(i = 0; i < len; str++, i++)
   {
      hash ^= ((i & 1) == 0)
         ? (  (hash <<  7) ^ (*str) * (hash >> 3))
         : (~((hash << 11) + ((*str) ^ (hash >> 5))));
   }

   return hash;
}
/* End Of AP Hash Function */

/*Hash string with 11 different hash function(flag = 0)
Or Search string in a maked bloom filter(flag = 1)
*/
int bloomfilter_insert(unsigned char * bitmap, char* emailstring, int flag){
	unsigned int index;

	index = RSHash(emailstring,strlen(emailstring)) % MAX;
	if(flag == 1){if(bitmap_get(bitmap,index) == 0) return 0;}
	else bitmap_set(bitmap,index,1);

	index = JSHash(emailstring,strlen(emailstring)) % MAX;
	if(flag == 1){if(bitmap_get(bitmap,index) == 0) return 0;}
	else bitmap_set(bitmap,index,1);

	index = PJWHash(emailstring,strlen(emailstring)) % MAX;
	if(flag == 1){if(bitmap_get(bitmap,index) == 0) return 0;}
	else bitmap_set(bitmap,index,1);

	index = ELFHash(emailstring,strlen(emailstring)) % MAX;
	if(flag == 1){if(bitmap_get(bitmap,index) == 0) return 0;}
	else bitmap_set(bitmap,index,1);

	index = BKDRHash(emailstring,strlen(emailstring)) % MAX;
	if(flag == 1){if(bitmap_get(bitmap,index) == 0) return 0;}
	else bitmap_set(bitmap,index,1);

	index = SDBMHash(emailstring,strlen(emailstring)) % MAX;
	if(flag == 1){if(bitmap_get(bitmap,index) == 0) return 0;}
	else bitmap_set(bitmap,index,1);

	index = DJBHash(emailstring,strlen(emailstring)) % MAX;
	if(flag == 1){if(bitmap_get(bitmap,index) == 0) return 0;}
	else bitmap_set(bitmap,index,1);

	index = DEKHash(emailstring,strlen(emailstring)) % MAX;
	if(flag == 1){if(bitmap_get(bitmap,index) == 0) return 0;}
	else bitmap_set(bitmap,index,1);

	index = BPHash(emailstring,strlen(emailstring)) % MAX;
	if(flag == 1){if(bitmap_get(bitmap,index) == 0) return 0;}
	else bitmap_set(bitmap,index,1);

	index = FNVHash(emailstring,strlen(emailstring)) % MAX;
	if(flag == 1){if(bitmap_get(bitmap,index) == 0) return 0;}
	else bitmap_set(bitmap,index,1);

	index = APHash(emailstring,strlen(emailstring)) % MAX;
	if(flag == 1){if(bitmap_get(bitmap,index) == 0) return 0;}
	else bitmap_set(bitmap,index,1);

	return 1;
}

测试部分略。

结语

实际操作中，Bloom Filter达到了和Trie一样的效果，且时间短，占用内存少。可见其效率。实际上，Bloom Filter已有诸多应用：

  • Google 著名的分布式数据库 Bigtable 使用了布隆过滤器来查找不存在的行或列，以减少磁盘查找的IO次数。
  • Squid 网页代理缓存服务器在 cache digests中使用了也布隆过滤器。
  • Venti 文档存储系统也采用布隆过滤器来检测先前存储的数据。
  • SPIN 模型检测器也使用布隆过滤器在大规模验证问题时跟踪可达状态空间。
  • Google Chrome浏览器使用了布隆过滤器加速安全浏览服务。

参考资料

  1. 维基百科：布隆过滤器
  2. 数学之美二十一：布隆过滤器（Bloom Filter）
  3. 布隆过滤器(Bloom Filter)详解 - Haippy - 博客园
  4. 海量数据处理算法—Bloom Filter
  5. 那些优雅的数据结构(1) : BloomFilter——大规模数据处理利器
  6. Bloom Filter算法详解及实例
  7. bitmap应用及C语言实现
  8. bitmap C语言实现
  9. General Purpose Hash Function Algorithms