Vue2.0的响应式设计原理
前言
上周抽空看了看Vue的源码,设计的精巧让我这个鶸一时吸收不来。如果想写篇既大又全的文章,一劳永逸地介绍Vue2.0的源码,以我的水平显然是做不到的。于是就只取一瓢饮地,简单记录下Vue2.0在响应式原理上的设计。其他的部分等我功力深厚了(其实就是懒)再做总结吧。
基础
这一部分是Vue响应式原理的基础。包含Observer类,Watcher类,Dep类,事件订阅模式,还有最关键的Object.defineProperty方法。
Object.defineProperty
Vue实现数据绑定的方式和其他的MVVM同侪不同,React和backbone(这货不是MVVM)采用的是典型的发布订阅模式,Angular则采用的脏值检测。
Vue使用了更为隐蔽和magical的Object.defineProperty设置对象访问器属性(这也意味着Vue只支持到IE9+)。
把一个普通 Javascript 对象传给 Vue 实例的 data 选项,Vue 将遍历此对象所有的属性,并使用 Object.defineProperty 把这些属性全部转为 getter/setter。Object.defineProperty 是仅 ES5 支持,且无法 shim 的特性,这也就是为什么 Vue 不支持 IE8 以及更低版本浏览器的原因。
Object.defineProperty()可以定义对象的访问器属性,关于访问器属性的更多介绍可以看这里。其中get和set方法分别用来指定属性的getter和setter。
1 | var person = { |
通过getter和setter实现数据劫持是Vue数据绑定的基础。
发布订阅
发布订阅是JavaScript中事件机制的实现方式,也是JavaScript异步编程的实现方式之一。
发布订阅模式中的角色主要有发布者、事件对象、订阅者。发布者和事件对象是一对多的关系,事件对象和订阅者又是一对多的关系。当发布者的状态改变触发事件对象时,相关的订阅者就会收到通知。实现起来就像下面这样。
1 | var EventUtil = { |
Vue实现视图自动更新的原理也是如此,当然细节上就复杂多了。
Observer,Watcher,Dep
这三个是相辅相成实现Vue数据绑定的组件。
Observer
Vue在组件(Component)初始化过程中,会将数据对象封装为Observer对象,便于监听数据的改变,并绑定依赖在上面。我们来看下源码。
1 | constructor (value: any) { |
Observer对象储存在 ob 这个属性,这个属性保存了 Observer 对象自己本身。对象在转化为 Observer 对象的过程中是一个递归的过程,对象的子元素如果是对象或数组的话,也会转化为 Observer 对象。
由于JavaScript本身的原因,Vue不能监测数组的变化,Vue采用的折中方法是增强数组的原生方法push, pop, shift, unshift, splice, sort, reverse,以及建议使用者通过Vue.set的方式显示调用。通过其他方式对数组进行的修改将无法被监听到。
Watcher
Vue中,Watcher和模板渲染紧密相连,它将Observer发生的改变反映到模板内容上。它关键部分的源码是这样。
1 | constructor ( |
其中输入参数vm是监听的组件,expOrFn最终将交给getter属性,cb是更新时的回调函数。最后一句中的this.get()完成了依赖的收集工作。
1 | /** |
第一句的pushTarget(this)设置了Dep.target,getter函数正是通过Dep.target是否为null,判断当前处于依赖收集阶段还是普通数据读取。后面的两句去touch``expOrFn涉及到的每个数据项。从而将expOrFn的依赖收集起来。最后将dep中的内容清空,为下次收集依赖做准备。
Dep
Dep类用于连接Watcher类和Observer类,每个Observer对象中都有一个Dep实例,其中存储了订阅者Watcher。源码如下:
1 | //... |
Dep类比较简单,主要是一个存储Watcher实例的数组this.subs。depend()方法用于向Watcher对象中添加这个Dep。notify()方法将遍历Watcher列表,通知订阅者更新视图。
实现
下面从源码角度上看看Vue实现数据绑定的设计。
目录结构
Vue核心部分的代码放在src目录。路径下还有下面这些子文件夹:
entries入口文件,根据编译环境的不同,更改一些配置compiler编译模板,render函数的实现core关键部分代码core/observer响应式设计中的Observer对象实现core/vdom虚拟DOM,diff算法,patch函数实现core/instance组件实例生命周期实现,组件初始化入口core/components全局组件core/global-api全局APIserver服务端渲染platform平台特定代码,分为web和weexsfc处理单文件组件 解析.vue文件share工具函数
生命周期
关于Vue的生命周期,这里假设你已经熟悉,就不做介绍了。了解它也将帮助你了解Vue的工作流程。
源码的入口从下面一行代码开始:
1 | function Vue (options) { |
文件为src/core/instance/index.js,关键在于最后一句,通过调用init.js中定义的_init(options)方法初始化Vue实例。这个方法是在下面的initMixin(Vue)中导入的。这种mixin的方式不同于Vue1.x版本,更具模块化适合拓展(同时也增加了寻找代码的难度)。
初始化相关的主要代码如下;
1 | function initMixin (Vue: Class<Component>) { |
initLifecycle主要是初始化vm实例上的一些参数;initEvents是事件监控的初始化;initRender是模板解析,2.0的版本中这一块有很大的改动,1.0的版本中Vue使用的是DocumentFragment来进行模板解析,而 2.0 中作者采用的John Resig的HTML Parser将模板解析成可直接执行的render函数。initState是数据绑定的主战场,我们下一节会详细讲到。callHook执行生命周期的钩子函数。
initState
在初始化中,initState函数承担了数据绑定中的最主要的脏活累活。它的源码像下面这样:
1 | export function initState (vm: Component) { |
可以看到,initState将工作拆解成观察props, data, methods, computed, watch几个关键部分。
initData
以initData方法为例,它是如何使用上面提到的Observer, Dep, Watcher类的呢,我们看看源码:
1 | function initData (vm: Component) { |
可以看到,这个函数做了下面的工作:
- 保证data为纯对象
- 检查是否与
props中属性有重复 - 进行数据代理,便于我们直接通过vm.xxx的形式访问原本位于vm._data.xxx的属性。
- 调用
observe方法对data进行包装,使之具有响应式的特点。
那我们看看observe方法是怎么写的吧
1 | /** |
observe方法主要就是判断value是否满足一些预设条件,并将这个对象转化为Observer对象。
关于Observer类我们上面已经提到,它的构造函数做了下面几个工作:
- 首先创建了一个Dep对象实例;
- 然后把自身this添加到value的
__ob__属性上; - 最后对value的类型进行判断,如果是数组则观察数组,否则观察单个元素(要理解这一步是个递归过程,即value的元素如果符合条件也需要转化为Observer对象)。
不论是基础类型还是数组或对象,最终都会走入到walk方法,方法定义在src/core/observer/index.js中。
1 | walk (obj: Object) { |
defineReactive
在经过一系列的准备工作和铺垫后,终于可以接触到数据绑定最核心部分的defineReactive函数。方法也定义在src/core/observer/index.js中,源码如下:
1 | /** |
defineReactive是对Object.defineProperty方法的包装,结合observe方法对数据项进行深入遍历,最终将所有的属性就转化为getter和setter。其中对于Dep的处理用于收集依赖data的Watcher对象。
依赖收集
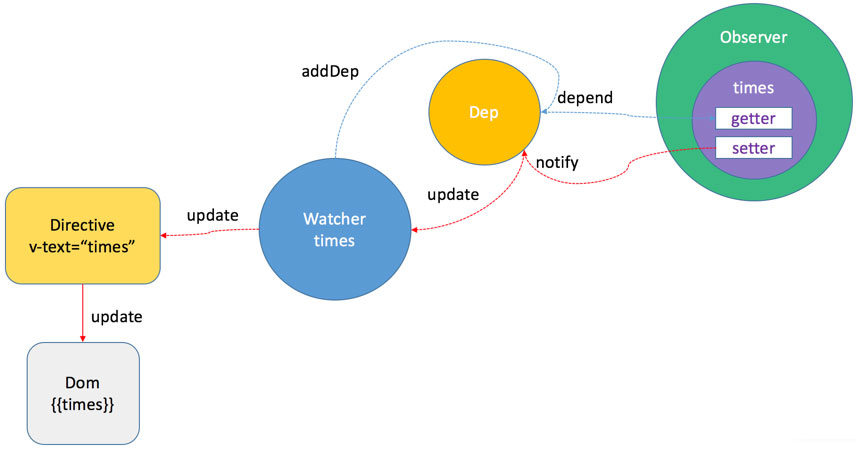
data的依赖收集是在getter函数中完成的。Observer和Dep是一对一的关系,Dep用来存储依赖Observer的Watcher。Dep和Watcher是多对多的关系,一个Dep中存储了若干Watcher,一个Watcher可能同时依赖于多个Observer。
可以看到Dep是连接Observer(生产者)和Watcher(消费者)的关键纽带。Watcher通过getter函数建立起和Observer中Dep的关联。在Observer的setter函数中会触发dep.notify()方法,根据上文对该方法的讲解,它实际上对数组中每个Watcher执行了update方法。在方法中根据是否同步去执行run方法,这个方法中通过源码可以看到实际上正是通过const value = this.get()获取最新的value。
1 | update () { |
- 模板编译过程中的指令和数据绑定都会生成 Watcher实例,watch函数中的对象也会生成 Watcher实例,在实例化的过程中,会调用watcher.js中的get函数touch这个Watcher的表达式或函数涉及的所有属性;
- touch开始之前Watcher会设置Dep的静态属性Dep.target指向其自身,然后开始依赖收集;
- touch属性的过程中,属性的getter函数会被访问;
- 属性gette 函数中会判断Dep.target(target中保存的是第2步中设置的Watcher实例)是否存在,若存在则将 getter函数所在的Observer 实例的Dep实例保存到Watcher的列表中,并在此Dep实例中添加Watcher为订阅者;
- 重复上述过程直至Watcher的表达式或函数涉及的所有属性均touch结束(即表达式或函数中所有的数据的getter函数都已被触发),Dep.target被置为null,依赖收集完成;
总结
上面尝试从源码角度对Vue2.0的响应式设计做了浅析。总结一下就是下面几点:
- 在生命周期的initState方法中对
data,prop,method,computed,watch方法中的数据进行劫持,通过defineReactive和observe将之转换为Observer对象 initRender函数中解析模板,新建Watcher对象通过Dep对象和对应数据建立了依赖关系,通过Dep.target这个全局对象判断是否是依赖收集阶段。- 数据变化时,通过
setter函数中的dep.notify方法执行Watcher的update方法更新视图